--------點擊屏幕右側或者屏幕底部“+訂閱”,關注我,隨時分享機器智能最新行業動態及技術乾貨----------

前言
與傳統工業優化不同,多智能體系統中每個機器人互相替代性很強,流程是非線性的,導致系統效率很難直接建模。一般通過調整任務分配與移動路徑,優化總任務距離來間接逼近系統效率。但我們在實踐中發現,任務距離與系統效率並不強相關。由於成本的限制,機器人數量往往是有限的,當針對任務距離進行優化時,會導致部分作業人員過於繁忙,而部分作業人員無事可做的問題。
因此我們結合了菜鳥柔性自動化實驗室在多智能體系統的實踐與反思,於論文《Idle Time Optimization for Target Assignment and Path Finding in Sortation Centers》中提出了基於工作站空閒時間的優化模型,關注如何最大化人的能力,從而推動整個系統達到更高的效率。我們對工作站的工作時間進行了離散化切分,模擬了機器人排隊與等待的情況,並通過一套統一的網絡流模型獲得機器人與工作站的分配策略,以及機器人集群的路徑規劃,提升了系統產能。
論文地址:https://aaai.org/Papers/AAAI/2020GB/AAAI-KouN.3001.pdf
應用場景
基於多智能體集群的自動化技術方案的興起和發展,促進了現代物流業的發展和全球化,代表著物流與供應鏈行業未來的一個主要方向。在阿里巴巴旗下菜鳥網絡以及其合作伙伴的倉儲和分撥中心有著成百上千的機器人在工作,實現包裹高效安全的到達用戶手上。

圖 1 機器人集群在分撥中心進行包裹分撥
圖 1 是一個機器人分撥中心,幾百個機器人在快速的把大量的包裹根據城市分撥,幫助幹線物流網絡更高效的運輸包裹。機器人分撥中心的核心是三部分:工作站(Station),機器人(Agent)以及道口(Sorting Bin)。機器人會自動行駛到工作站領取包裹,通過自動掃碼,然後再將包裹運輸到對應的目的地道口,此時機器人會將包裹投進道口,從而完成包裹分撥。如何讓這幾百個機器人高效的運轉,使得包裹可以更加快速的到達用戶手中。這裡要值得思考的是,一般性的會認為讓這些機器人總的行駛路線最短就會使得整個分撥中心的效率最高。然而並不是這樣,我們會看輸入和輸出,輸入是所有的包裹,輸出是各個道口中的包裹。受限於大量的包裹以及有限的機器人,僅僅是去優化路線最短並不能最大產出,這樣就會存在部分工作站機器人排隊而另一些工作站缺乏機器人的情況,在輸入部分就已經限制了整個系統的產能。所以我們的目標是最小化所有工作站的空閒時間,來達到最大化系統產能的目的。下面會介紹如何建模來解決最小化空閒時間的問題。
問題建模
我們將上圖機器人分撥中心模式進行抽象成如下圖 2 所示,這樣可以方便的引入多智能體路徑規劃的研究,其中核心三要素分別是橙色的工作站,綠色的機器人以及藍色的道口。
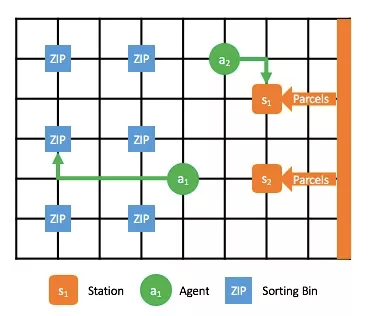
圖 2 分撥過程,橙色節點為工作站,綠色節點是機器人,藍色節點為分撥道口(每個道口對應了一個目的地結合)
要完成最小化工作站空閒時間,其核心是解決兩個問題:
- 每個機器人去哪個工作站接包裹,即任務分配(Task Assignment)問題;
- 接完包裹後每個機器人按照什麼路線運行到目的地道口,每個機器人可以視為一個智能體,即多智能體路徑規劃(Multi-Agent Path Finding, MAPF)問題。
這兩個問題合在一起在學術上定義為 TAPF 問題。解決單次的任務分配和路徑規劃問題,我們定義為一個單次的 TAPF 問題。那麼順理成章的對於上述的自動化分撥中心持續作業的場景,可以抽象成 Lifelong TAPF 問題。接下來我們給出 TAPF 的定義。在給定的如下 3 個條件:
- 一個全連接的無向圖 G(V,E);
- N個Station
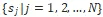 ;
; - M個Agent
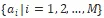 ;
;
TAPF 會找到一個分配方案,這個分配方案表示即為每個 Agent 去哪個 Station,同時會為所有的 Agents 找到沒有衝突的路徑使得可以更快的到達各自的工作站。
當每個 Agent 到達其目的地 Station 點後,Station 將需要T的時間將包裹處理到 Agent 上的時間。因此如果給定一個時間窗口 [0, KT),那麼我們可以設定每個工作站的操作時間為 K 個工作時間片: [0,T), [T,2T),..., [(K-1)T,KT),且每個 Station 僅允許 Agent 的到達時間為 kT,其中 k=0,1,...,K-1。基於以上,我們認為當一個 Agent 在 kT 時刻到達其目的地工作站時,則這個工作站在時間段 [kT,(k+1)T) 內將會被佔用。
對於 Life-Long TPAF 問題,那就不是僅僅計算一次任務分配和多智能體路徑規劃問題。其本質就是不斷的計算並更新每個 Agent 的分配方案和路徑,這樣對於上述場景中即是,每個機器人在運行過程中都在調整其目的地工作站和運行的路線,最終達到最小化工作站空閒時間最大化分撥中心產能的目的。
目標函數:基於以上定義,我們可以定義:在一個給定時間段內,最小化總的空閒時間,即為在這段時間內所有工作站的空閒時間之和。
示例說明:在後面的章節中,我們將用如下示例來詳細解釋每一種模型。
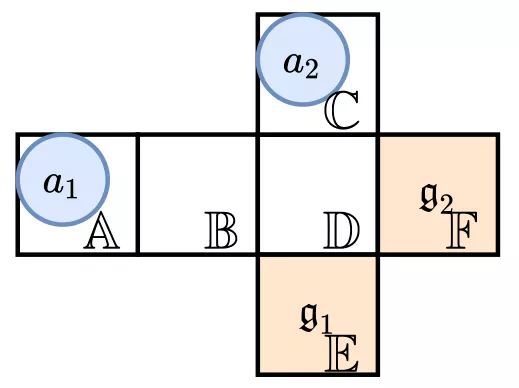
圖 3 問題示例
- 兩個 Agent:
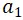 於時刻 0 從 A 出發,
於時刻 0 從 A 出發, 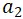 於時刻 1 於 C 出發;
於時刻 1 於 C 出發; - 兩個 Station:
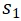 位於 E 點,其位置用
位於 E 點,其位置用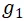 表示,
表示,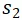 位於F點,其位置用
位於F點,其位置用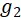 表示;
表示;
那麼假設給定時間範圍是 [0,6),工作站的處理時間 T=2,我們可以看到一個最優的 TAPF 的解決方案是給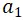 分配工作站
分配工作站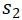 ,且其路線為 ;
,且其路線為 ;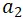 分配到工作站
分配到工作站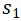 ,且其路線為 ,null 表示 0 時刻
,且其路線為 ,null 表示 0 時刻 不在地圖中。這樣兩個工作站的工作時間段均為 [4,6),得到的目標函數即總的空閒時間為 8。
不在地圖中。這樣兩個工作站的工作時間段均為 [4,6),得到的目標函數即總的空閒時間為 8。
ITO-空閒時間優化
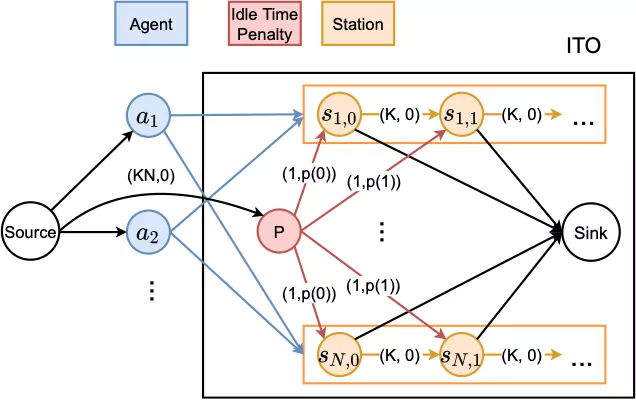
圖 4 ITO 模型,邊上標記(cost, capacity),為簡潔起見(cost=0,capacity=1)的邊沒有標記
為優化空閒時間,如圖 4 所示,我們建立了 ITO(Idle Time Optimization)網絡流模型。每一條邊有兩個屬性 (cost, capacity),cost 代表了每單位流量經過這條邊需要付出的代價,capacity 代表這條邊能承載多少單位的流量。為簡潔起見,在圖中我們省略(cost=0,capacity=1)的邊。
我們對每一個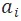 建立了一個對應的藍色節點,對每個
建立了一個對應的藍色節點,對每個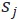 建立一個矩形 Station 子結構。Station 子結構根據時間軸展開成K個離散的時間段,每個時間段 [kT,(k+1)T) 用節點
建立一個矩形 Station 子結構。Station 子結構根據時間軸展開成K個離散的時間段,每個時間段 [kT,(k+1)T) 用節點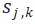 表示,這樣可以方便的考慮每個時間段的工作情況。Agent 與 Station 子結構之間是一個全連通的二分圖,表示每個 Agent 都能被指派到任意一個 Station 並佔用一個對應的工作時間段。
表示,這樣可以方便的考慮每個時間段的工作情況。Agent 與 Station 子結構之間是一個全連通的二分圖,表示每個 Agent 都能被指派到任意一個 Station 並佔用一個對應的工作時間段。

圖5 Agent 節點與 Station 子結構的鏈接
圖 5 解釋了 Agent 節點與 Station 子結構的鏈接細節。對於每一組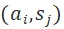 ,我們可以估算
,我們可以估算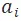 到達
到達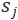 的時間,如果這個時間段是[kT,(k+1)T),那麼
的時間,如果這個時間段是[kT,(k+1)T),那麼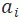 可以在
可以在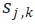 時間段開始排隊,並填補之後任意一個時間段的空缺,排隊的特性我們通過
時間段開始排隊,並填補之後任意一個時間段的空缺,排隊的特性我們通過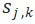 與
與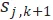 之間的鏈接實現。
之間的鏈接實現。
最後,為使得整個系統的空閒時間最少,我們希望找到一個工作站指派使得工作站時間段儘可能被佔用。因此我們以 Agent 節點為流的入口,每個 Agent 分配一個單位流量,以工作站時間段為出口,每個工作時間段最多流出一個單位流量。這樣每個時間段只能被一個 Agent 獨佔,每個 Agent 也只能佔用一個時間段。這個網絡流模型的最大流解即是使整個系統空閒時間最少的 Agent-Station 分配。當我們得出分配方案後,再通過 MAPF 算法求得無衝突的 Agent 路徑,就可以按照該路徑來控制調度整個多智能體集群。
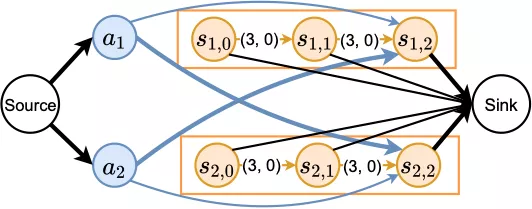
圖6 示例的 ITO 模型
圖 6 是前文示例對應的 ITO 模型,兩個 Agent 的預測到達時間都是在第 3 個時間段,粗邊是最大流的解,對應匹配為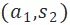 與
與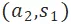 。
。
PITO-結合路徑規劃的空閒時間優化
由於 ITO 將 Station 分配與路徑規劃分開考慮,其效果高度依賴於基於到達時間預測的精確程度。為了避免這個依賴,我們基於 ITO 設計了 PITO(Path Finding with ITO),它將 ITO 與匿名 MAPF 網絡流模型(Anonymous MAPF flow network, Yu and LaValle 2013)相結合,通過一個統一個網絡流模型,同時計算得出 Station 分配與 Agent 路徑。
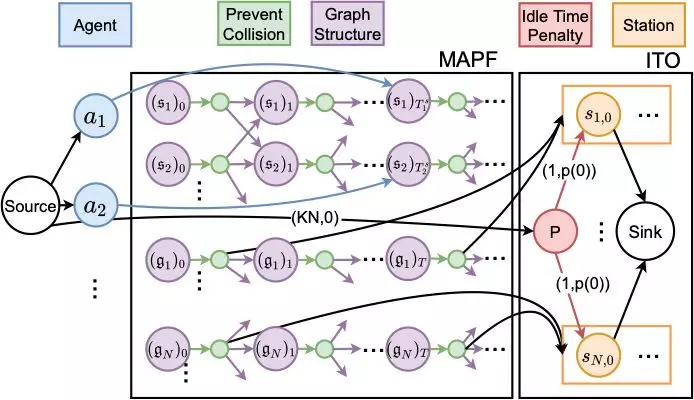
圖 7 PITO 模型
PITO 的構造過程如圖7所示由兩部分構成。左側 MAPF 網絡用於計算生成路徑信息,右側 ITO 網絡用於生成 Station 分配結果。
對於任何一個地圖中的點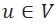 ,我們根據時間軸將其擴展到每一時刻 t,t 時刻的 u 用一個紫色節點
,我們根據時間軸將其擴展到每一時刻 t,t 時刻的 u 用一個紫色節點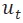 表示。對於每一個
表示。對於每一個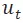 ,我們創建一個緊隨其後的綠色輔助節點
,我們創建一個緊隨其後的綠色輔助節點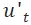 。由於
。由於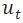 與
與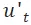 之間只有一條 capacity 為 1 的邊,任何時刻 t 最多隻會有一個單位的流通過 u,從而避免了多個 Agent 同時到達 u 而相撞。我們在這裡並沒有在網絡結構中設計避免在邊上相撞,而是採用了一個小技巧,如果有兩個 Agent 在一條邊上相撞,則令他們在當前點等待,並交換兩者的 Station 分配與後面的路徑。由於 Agent 是匿名的,交換 Station 分配與後面的路徑並不會影響空閒時間,從而達到了簡化網絡、加速求解的目的。
之間只有一條 capacity 為 1 的邊,任何時刻 t 最多隻會有一個單位的流通過 u,從而避免了多個 Agent 同時到達 u 而相撞。我們在這裡並沒有在網絡結構中設計避免在邊上相撞,而是採用了一個小技巧,如果有兩個 Agent 在一條邊上相撞,則令他們在當前點等待,並交換兩者的 Station 分配與後面的路徑。由於 Agent 是匿名的,交換 Station 分配與後面的路徑並不會影響空閒時間,從而達到了簡化網絡、加速求解的目的。
ITO 網絡和前一章的構造方式基本相同,我們不再將Agent 與 Station 子結構直接相連,而是採用讓 Agent 通過 MAPF 直接“走到” Station 的方式。每個 Station 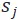 有其真實位置
有其真實位置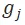 。對於每個工作時間段 [kT,(k+1)T),我們從輔助節點
。對於每個工作時間段 [kT,(k+1)T),我們從輔助節點 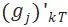 連接一條邊到對應的工作站時間段
連接一條邊到對應的工作站時間段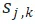 ,從而允許Agent在到達
,從而允許Agent在到達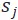 時可以佔用其對應工作時間段。最後我們根據 Agent 的起始時間與起始位置,將它們連接到對應的節點上。
時可以佔用其對應工作時間段。最後我們根據 Agent 的起始時間與起始位置,將它們連接到對應的節點上。
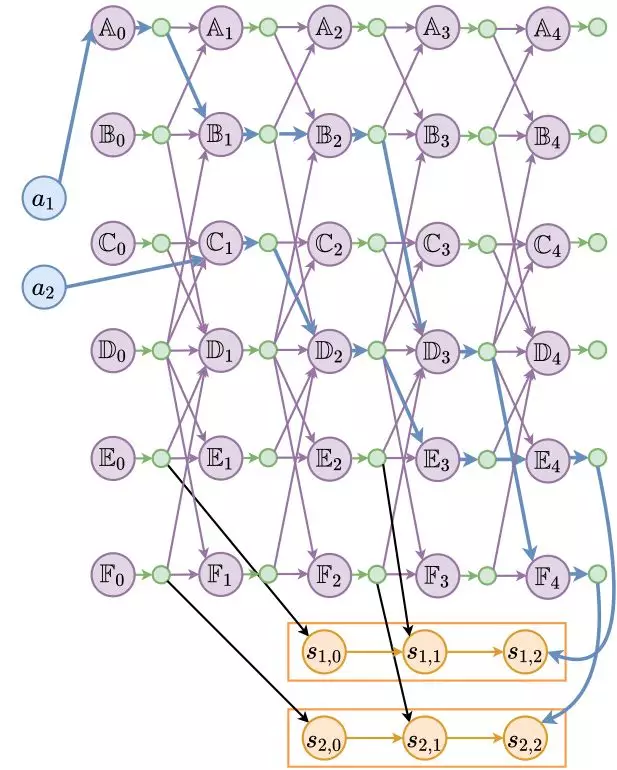
圖8 示例的 PITO 模型
圖8 是前文示例對應的 PITO 模型,藍色粗邊相連的節點展示了 Agent 的對應路徑以及 Station 的分配結果。
Lifelong 優化
這一章我們討論如何將 ITO 與 PITO 應用到 Lifelong 的優化中。前面我們討論瞭如何利用 ITO 與 PITO 求解 One-Shot 問題的 Station 分配與路徑規劃,每個 Agent 只需要去 Station 一次。但在現實場景中我們更關心的是一個動態的過程,Agent 不斷往返工作站與傾倒口。因此在每經過 的一個時間窗口,我們會重新根據場上情況重算為 Agent 分配 Station 並規劃路徑。
但為了讓上個時間窗口的結果能夠更好的為下一個時間窗口留出優化空間,Agent 最好能佔用更早工作時間段。我們通過增加懲罰節點 P 來達到這個目的。如圖 4 和 8,我們在 ITO 與 PITO 中增加了一個紅色懲罰節點 P,將它們轉化為一個最小費用最大流的問題。P 擁有足夠大的流量並且跟所有的時間段相連但 cost 不為 0,如果一個工作時間段沒有 Agent 能夠佔據,就會產生一個從 P 到該時間段的等同於 cost 的懲罰。為了讓 Agent 儘可能佔據前面的時間段,我們用一個隨時間單調遞減的函數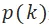 來表示P到
來表示P到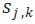 的cost,比如採用線性遞減或者指數遞減函數。從而當空閒時間相等時,解會傾向於將空閒時間放在後面。
的cost,比如採用線性遞減或者指數遞減函數。從而當空閒時間相等時,解會傾向於將空閒時間放在後面。
我們將 Lifelong 版的 ITO 與 PITO(帶時間窗口 W 與懲罰節點 P)稱為 ITO-L 與 PITO-L。
實驗分析
基於以上提出的的 ITO-L 和 PITO-L 算法以及我們給出3種對比算法,共 5 種算法框架進行 Life-Long TAPF 的實驗對比。5 種算法框架分別如下:
-
1)H(Inf)-L
採用 Hungarian 算法將所有 agents 按照總距離最近的方式統一分配到工作站,解決 Task Assignment 問題,然後採用改進的 PBS 算法求解 MAPF 問題;隨著系統的運行不斷重複實時的計算直至時間窗口結束。
-
2)H(1)-L
採用Hungarian算法重複計算 [M/N] 次將所有 agents 分配到工作站,解決 Task Assignment 問題;然後採用改進的 PBS 算法求解 MAPF 問題,隨著系統的運行不斷重複實時的計算直至時間窗口結束。
-
3)H(Q)-L
採用 Hungarian 算法重複計算 [M/(NQ)] 次將所有 agents 分配到工作站,解決 Task Assignment 問題;然後採用改進的 PBS 算法求解 MAPF 問題。可以發現 H(1)-L 和 H(Inf)-L 分別對應 Q=1 和 Q=∞,隨著系統的運行不斷重複實時的計算直至時間窗口結束。
-
4)ITO-L
採用 Primal Dual 算法求解 Min Cost Max Flow 問題,解決 Task Assignment 問題;然後採用改進的 PBS 算法求解 MAPF 問題,隨著系統的運行不斷重複實時的計算直至時間窗口結束。
-
5)PITO-L
採用 Primal Dual 算法求解可直接得到 TAPF 問題的解,同時解決 Task Assignment 和 MAPF 問題,隨著系統的運行不斷重複實時的計算直至時間窗口結束。
下面將介紹我們採用的兩個實驗平臺。
Agent Simulator

圖9 模擬實驗中兩個分撥中心的地圖
Agent simulator 是指在我們隨機生成的分撥中心業務模式的地圖集合上(如圖 9 所示),其中橙色代表工作站,藍色表示道口,Agent 未標明在上述地圖中。採用我們設計的仿真框架來模擬系統的運行,核心參數分別是:
- 工作站處理包裹時間,T = 10;
- 時間窗口範圍為[0,600],即KT = 600,K = 60;
- 每次重複計算的時間間隔30,即W = 30;
- Q = M/N + 5;
Industrial Simulator

圖10 分撥中心場地的 2D 佈局,綠點為 Station,灰點為不可達區域,黑點為道口
我們將 ITO-L 算法和 H(Q)-L 算法應用到上述應用場景的分撥中心的調度系統中;其中 Task Assignment 問題分別用對應的算法解決,實際中的路徑規劃採用 centralized A*算法求解以及解決 deadlock 問題。我們將實際分撥中心的地圖抽象抽象成如圖 10 所示。核心參數分別如下:
- T = 4;
- K = 75;
- Q = 15;
數據結果
Agent Simulator 的實驗結果如下圖 11 與 12 所示:
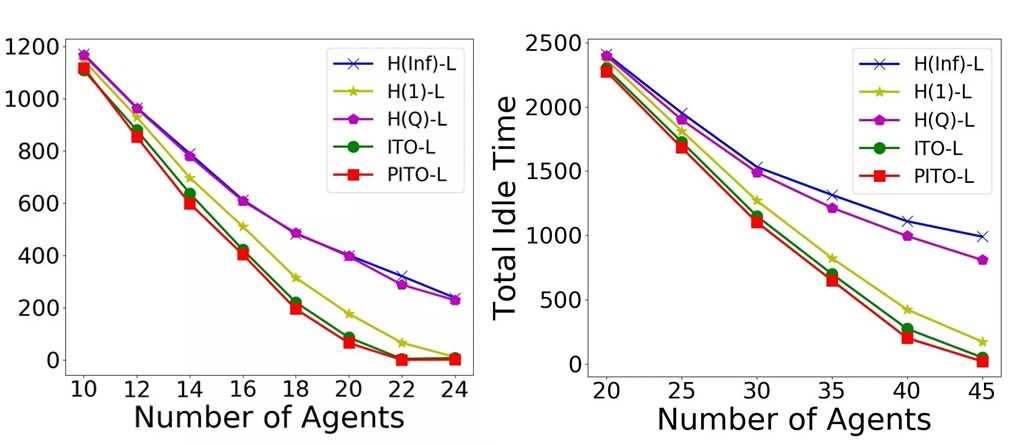
圖 11 變化 Agent 數量的空閒時間趨勢
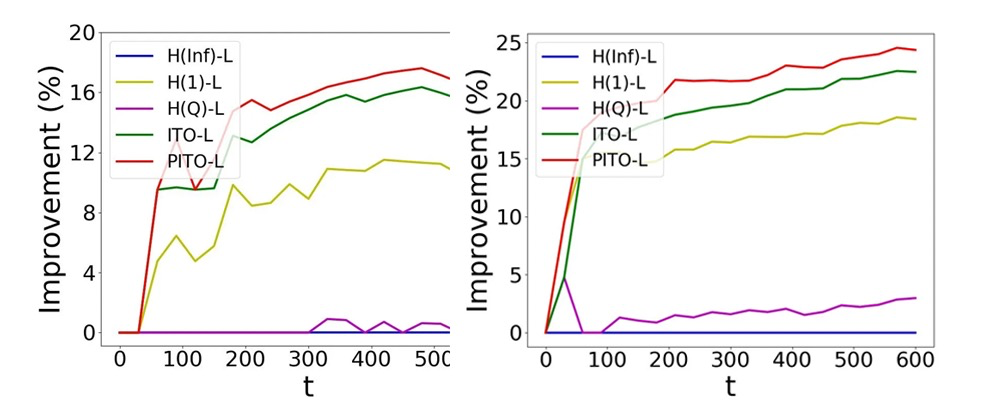
圖 12 相對H(Inf)-L算法,各算法對於總產能的提升比例
Industrial Simulator 的實驗結果如圖 13 所示,其中全場分佈的綠色方塊表示帶著包裹的機器人,全場分佈的藍色表示空載的機器人。

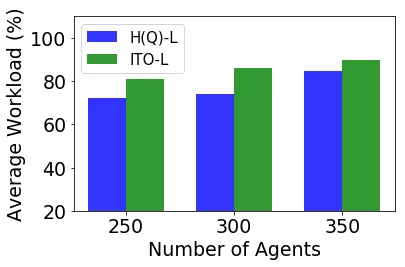
圖 13 Industrial Simulator 運行截圖,以及 ITO-L 與 H(Q)-L 在 Industrial Simulator 的表現
從以上數據結果我們可以看到:
- 在自測平臺上,無論是 ITO-L 還是 PITO-L 表現的要比其他算法好,最小化空閒時間帶來的產能提升超過 10%,且我們知道 10% 的分撥能力的提升對一個持續運行的業務系統來說已經是比較好的表現。
- 在實際分撥中心的系統仿真中,我們的產能提升也可以達到 11%,表明了我們所設計的算法的擴展性和實用性。
結束語
本文是研究任務分配,多智能體路徑規劃以及兩者結合在一起的 TAPF 問題的一次成功嘗試。我們的核心是針對當前物流行業前沿的自動化方案機器人作業模式的研究,分析其核心點 Life-Long TAPF 問題,首次提出了最小化工作站空閒時間的思想,來優化提高系統的效率。並在此基礎上設計了兩種算法框架 ITO-L 和 PITO-L 來求解 Lifelong TAPF 問題,達到最小化工作站空閒時間的目的。在實驗部分,我們分別採用了 Agent Simulator 和 Industrial Simulator 兩種仿真平臺來驗證所設計的兩種算法。實驗數據表明在兩個測試平臺上我們所提出的算法在系統產能上均可以有 10% 以上的提升,而對於一個長期運行的自動化作業系統來說,10% 的提升已經是一個不錯的表現,可以讓大量的包裹更加高效快速的到達用戶手中,對保證和提高物流時效、加速物流自動化的發展起到了積極的作用。本文主要表達,針對物流自動化機器人作業模式,我們在優化方向上和算法設計上的一些思考和做的事情。後續我們將繼續分析行業問題,設計和改進算法來進一步加速算法應用來提高系統效率。
