上一次我们一起学习了 GBDT 算法的回归部分,今天我们继续学习该算法的分类部分。使用 GBDT 来解决分类问题和解决回归问题的本质是一样的,都是通过不断构建决策树的方式,使预测结果一步步的接近目标值。
因为是分类问题,所以分类 GBDT 和回归 GBDT 的 Loss 函数是不同的,具体原因我们在《深入理解逻辑回归》 一文中有分析过,下面我们来看下分类 GBDT 的 Loss 函数。
Loss 函数
和逻辑回归一样,分类 GBDT 的 Loss 函数采用的也是 Log Likelihood:
$$
L = \arg\min\left[\sum_i^n-( y_i\log(p_i)+(1-y_i)\log(1-p_i) )\right]
$$
其中,n 表示有 n 条样本,$y_i$ 为第 i 条样本的观察值(或目标值),该值要么是 0,要么是 1; $p_i$ 为模型对第 i 个样本的预测值,它是一个取值范围为 [0,1] 之间的概率,现在我们来看下该 Loss 是否可导,只用看"求和符号 $\sum$" 里面的部分是否可导即可,如下:
$$
\begin{aligned}
l&=-y_i\log(p_i) - (1-y_i)\log(1-p_i)\\
&=-y_i\log(p_i)-\log(1-p_i)-y_i\log(1-p_i)\\
&=-y_i(\log(\frac{p_i}{1-p_i}))-\log(1-p_i)
\end{aligned}
$$
把上面式子中的 p 用 log(odds) 来表示,即用 $\log(odds_i)$ 来替换 $\log(p_i/(1-p_i))$,用 $e^{\log(odds_i)}/(1+e^{\log(odds_i)})$ 来替换 $p_i$(对 log(odds) 不熟悉的同学,可以先阅读深入理解逻辑回归一文),如下:
$$
\begin{aligned}
l&= -y_i\log(odds_i) - \log(1-\frac{e^{\log(odds_i)}}{1+e^{\log(odds_i)}})
\\&=- y_i\log(odds_i) - \log(\frac{1}{1+e^{\log(odds_i)}})
\\&=-y_i\log(odds_i)+\log(1+e^{\log(odds_i)})
\end{aligned}
$$
我们再对其求导:
$$
\frac{dl}{d\log(odds)} = -y_i + \frac{e^{\log(odds_i)}}{1+e^{\log(odds_i)}}
$$
右边的 $e^{log(odds_i)}/(1+e^{log(odds_i)})$ 正好又是 $p_i$,所以 $l'(\log(odds))$ 又等于 $-y_i+p_i$,注意,这两种形式后面都会用到。可见,这个 loss 函数是可导的,该分类算法可以用梯度下降来求解。
构建分类 GBDT 的步骤依然是下面两个:
- 初始化 GBDT
- 循环生成决策树
下面我们来一一说明:
初始化 GBDT
和回归问题一样,分类 GBDT 的初始状态也只有一个叶子节点,该节点为所有样本的初始预测值,如下:
$$
F_0(x) = \arg\min_{\gamma}\sum_{i=1}^n L(y,\gamma)
$$
上式中,F 代表 GBDT 模型,$F_0$ 为模型的初始状态,该式子意为:找到一个 $\gamma$,使所有样本的 Loss 最小,在这里及下文中,$\gamma$ 都表示节点的输出,且它是一个 log(odds) 形式的值,在初始状态,$\gamma$ 又是 $F_0$。
我们还是用一个最简单的例子来说明该步骤,假设我们有以下 3 条样本:
| 喜欢爆米花 | 年龄 | 颜色偏好 | 喜欢看电影 |
|---|---|---|---|
| Yes | 12 | Blue | Yes |
| No | 87 | Green | Yes |
| No | 44 | Blue | No |
我们希望构建 GBDT 分类树,它能通过「喜欢爆米花」、「年龄」和「颜色偏好」这 3 个特征来预测某一个样本是否喜欢看电影,因为是只有 3 个样本的极简数据集,所以我们的决策树都是只有 1 个根节点、2 个叶子节点的树桩(Stump),但在实际应用中,决策树的叶子节点一般为 8-32 个。
我们把数据代入上面的公式中求 Loss:
$$
Loss = L(1,\gamma)+L(1,\gamma)+L(0,\gamma)
$$
为了使其最小,我们对它求导,并令结果等于 0:
$$
(-1+p)+(-1+p)+(0+p)=0
$$
于是初始值 $p=2/3=0.67$,$\gamma=\log(2)=0.69$,模型的初始状态 $F_0(x)$ 为 0.69。
说了一大堆,实际上你却可以很容易的算出该模型的初始值,它就是正样本数比上负样本数的 log 值,例子中,正样本数为 2 个,负样本为 1 个,那么:
$$
F_0(x)=\log(\frac{positive\_count}{negative\_count}) = \log(\frac{2}{1}) = 0.69
$$
循环生成决策树
和回归 GBDT 一样,分类 GBDT 第二步也可以分成四个子步骤:(A)、(B)、(C)、(D),我们把它写成伪代码:
for m = 1 to M:
(A)
(B)
(C)
(D)其中 m 表示第 m 棵树,M 为树的个数上限,我们先来看 (A):
(A):计算
$$
r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)}
$$
此处为使用 m-1 棵树的模型,计算每个样本的残差 $r_{im}$,这里的偏微分实际上就是求每个样本的梯度,因为梯度我们已经计算过了,即 $-y_i+p_i$,那么 $r_{im}=y_i-p_i$,于是我们的例子中,每个样本的残差如下:
| 样本 i | 喜欢看电影 | 第1棵树的残差 $r_{i1}$ |
|---|---|---|
| 1 | Yes | 1-0.67=0.33 |
| 2 | Yes | 1-0.67=0.33 |
| 3 | No | 0-0.67=-0.67 |
这样,第 (A) 小步就完成了。
(B):使用回归树来拟合 $r_{im}$,回归树的构建过程可以参照《CART 回归决策树》一文。我们产生的第 2 棵决策树(此时 m=1)如下:
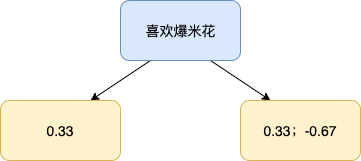
(C):对每个叶子节点 j,计算
$$
\gamma_{jm} = \arg\min_{\gamma}\sum_{x\in R_{ij}} L(y_i, F_{m-1}(x_i) + \gamma)
$$
意思是,在刚构建的树 m 中,找到每个节点 j 的输出 $\gamma_{jm}$,能使该节点的 Loss 最小。
左边节点对应第 1 个样本,我们把它带入到上式得:
$$
L(y_1,F_{m-1}(x_1)+\gamma)=-y_1(F_{m-1}(x_1)+\gamma) + \log(1+e^{F_{m-1}(x_1)+\gamma})
$$
对上式直接求导较为复杂,这里的技巧是先使用二阶泰勒公式来近似表示该式,再求导:把 $\gamma$ 作为变量,其余项作为常量的二阶泰勒展开式如下:
$$
L(y_1,F_{m-1}(x_1)+\gamma)\approx L(y_1,F_{m-1}(x_1)) + L'(y_1,F_{m-1}(x_1))\gamma + \frac{1}{2}L''(y_1,F_{m-1}(x_1))\gamma^2
$$
这时再求导就简单了:
$$
\frac{dL}{d\gamma} = L'(y_1,F_{m-1}(x_1)) + L''(y_1,F_{m-1}(x_1))\gamma
$$
Loss 最小时,上式等于 0,于是我们可以求出 $\gamma$
$$
\gamma_{11} = \frac{-L'(y_1,F_{m-1}(x_1))}{L''(y_1,F_{m-1}(x_1))}
$$
可以看出,上式的分子就是残差 r,下面我们算一下分母,即 Loss 函数的二阶微分:
$$
\begin{aligned}
L''(y_1,F(x)) &= \frac{dL'}{d\log(odds)}\\
&=\frac{d}{d\log(odds)}\left[-y_i + \frac{e^{\log(odds)}}{1+e^{\log(odds)}}\right]\\
&=\frac{d}{d\log(odds)}\left[e^{\log(odds)}(1+e^{\log(odds)})^{-1}\right]\\
&=e^{\log(odds)}(1+e^{\log(odds)})^{-1} - e^{2\log(odds)}(1+e^{\log(odds)})^{-2}\\
&=\frac{e^{\log(odds)}}{(1+e^{\log(odds)})^2}
\end{aligned}
$$
我们知道,$e^{\log(odds)}/(1+e^{\log(odds)})$ 就是 p,而 $1/(1+e^{\log(odds)})$ 是 1-p,所以 $L''=p(1-p)$,那么该节点的输出就是
$$
\gamma_{11} = \frac{r_{11}}{p_{10}(1-p_{10})}=\frac{0.33}{0.67\times0.33} = 1.49
$$
接着我们来计算右边节点的输出,它包含样本 2 和样本 3,同样使用二阶泰勒公式展开:
$$
\begin{aligned}
&L(y_2,F_{m-1}(x_2)+\gamma) + L(y_3,F_{m-1}(x_3)+\gamma)\\
&\approx L(y_2,F_{m-1}(x_2)) +L'(y_2,F_{m-1}(x_2))\gamma + \frac{1}{2}L''(y_2,F_{m-1}(x_2))\gamma^2\\
&+L(y_3,F_{m-1}(x_3)) +L'(y_3,F_{m-1}(x_3))\gamma + \frac{1}{2}L''(y_3,F_{m-1}(x_3))\gamma^2
\end{aligned}
$$
对上式求导,令其结果为 0,可以计算 $\gamma$ 为
$$
\begin{aligned}
\gamma_{21} &= \frac{-L'(y_2,F_{m-1}(x_2))-L'(y_3,F_{m-1}(x_3))}{L''(y_2,F_{m-1}(x_2))+L''(y_3,F_{m-1}(x_3))}\\
&=\frac{r_{21}+r_{31}}{p_{20}(1-p_{20}) + p_{30}(1-p_{30})}\\
&=\frac{0.33-0.67}{0.67\times 0.33 + 0.67\times 0.33}\\
&= -0.77
\end{aligned}
$$
这样,(C) 步骤即完成了。可以看出,对任意叶子节点,我们可以直接计算其输出值:
$$
\gamma_{jm} = \frac{\sum_{i=1}^{R_{ij}} r_{im}}{\sum_{i=1}^{R_{ij}} p_{i,m-1}(1-p_{i,m-1})}
$$
(D):更新模型 $F_m(x)$
$$
F_m(x) = F_{m-1}(x) + \nu \sum_{j=1}^{J_m} \gamma_m
$$
仔细观察该式,实际上它就是梯度下降——「加上残差」和「减去梯度」这两个操作是等价的,这里设学习率 $\nu$ 为 0.1,则 3 个样本更新如下:
| 样本 | 喜欢看电影 | $F_0(x)$ | $F_1(x)$ |
|---|---|---|---|
| 1 | Yes | 0.69 | 0.69+0.1×(1.49)=0.84 |
| 2 | Yes | 0.69 | 0.69+0.1×(-0.77)=0.61 |
| 3 | No | 0.69 | 0.61+0.1×(-0.77)=0.61 |
可见,样本 1 和样本 3 都离正确的方向更进了一步,虽然样本 2 更远了,但我们可以造更多的树来弥补该差距。
最终,循环 M 次后,或总残差低于预设的阈值时,我们的分类 GBDT 建模便完成了。
总结
本文主要介绍了分类 GBDT 的原理,具体有以下 2 个方面:
- 分类 GBDT 的 Loss 函数
- 构建分类 GBDT 的详细步骤
本文的公式比较多,但稍加耐心,你会发现它其实并不复杂。
参考: