一、問題簡述
BIM審核項目中,在建築模型數據入庫後,經常有模型構件進行投影的場景,模型投影調用超圖Supermap iObjects Java提供的GeoModel3D.converToRegion()接口。而當對某些複雜的模型構件(節點數目過多)進行投影操作時,運算效率較低,有時超過30分鐘。經過項目組的優化,有一定的優化效果,但是並沒有徹底改善這個問題。
如下圖所示的來源於某橋樑模型的構件,以三角形網格表達,該模型共有173926個節點和346459個面。
成功運行構件投影測試腳本,在windows虛擬機上運行時間大約為16分鐘,合960s。
二、問題分析
2.1現象觀察
從這個圖像中,我們有下述兩點觀察:
①真正對投影面積有較大影響的底面結構比較簡單,可以清晰地看到網格。
②所佔數據較大的,其實是圖中的圓柱體結構。如果利用超圖接口進行計算,輸入數據是進行過座標轉換到WGS84的三維座標數據。耗時的方法是GeoModel3D.convertToRegion()方法。該方法執行時間超過16分鐘,通過該方法計算後並轉換回投影座標系中計算出來的面積為5339370351平方毫米。
針對這一問題,首先可以嘗試尋找超圖接口的替代方法;除此之外,也可嘗試探索對原有網格進行簡化後再進行算法的方法。
2.2方案選定
經過多方資料查詢,嘗試從網格簡化和shapely庫地理計算的兩個角度出發解決該問題。
2.2.1基於Shapely的自行實現
經過討論,技術團隊認為本問題可以抽象為兩個步驟:
①第一步將三維模型中的所有節點都投影至XY平面,並完整的保留三角形網格,此時三角形網格會在同一個XY座標發生重疊。
②第二步針對超多數量的三角形網格進行一元聚合(unary_union),即在三角形重合的地方進行合併。合併之後即可以調用聚合後的二維圖形的面積接口,計算出投影面積。
具體實現上,第一步比較簡單,直接忽略z軸座標,並按照三角形網格的相同接口組成polygon即可以;第二步利用到的則是python shapely庫的unary_union接口, 該接口是GEOS庫中UnaryUnionOp類的簡單封裝。
面積的計算結果為5340510605平方毫米,與超圖的計算結果僅有1.14平方米的誤差。鑑於超圖的計算過程中從原始數據進行了座標轉換後又轉換回來,懷疑是這個過程中有精度損失。
在同一臺機器的相同的計算環境下,計算時間則大幅度減少到158s,僅僅是原來的16.5%。
2.2.2網格簡化算法
經過調研,學術界在網格簡化問題上影響力比較大的是卡內基梅隆大學在20世紀末提出的基於Quadric Error Metrics的算法。16年發佈的開源軟件MeshLab基於VCG Library對該算法有一個實現(功能名稱為Quadric Edge Collapse Decimation),因此可以藉助該軟件對簡化後再進行計算的思路進行驗證。而且MeshLib提供了cmdline的接口,從而使得該算法能力能夠簡單地被嵌入系統;或者可以直接包裝VCG Library的相關接口,接入該算法能力。
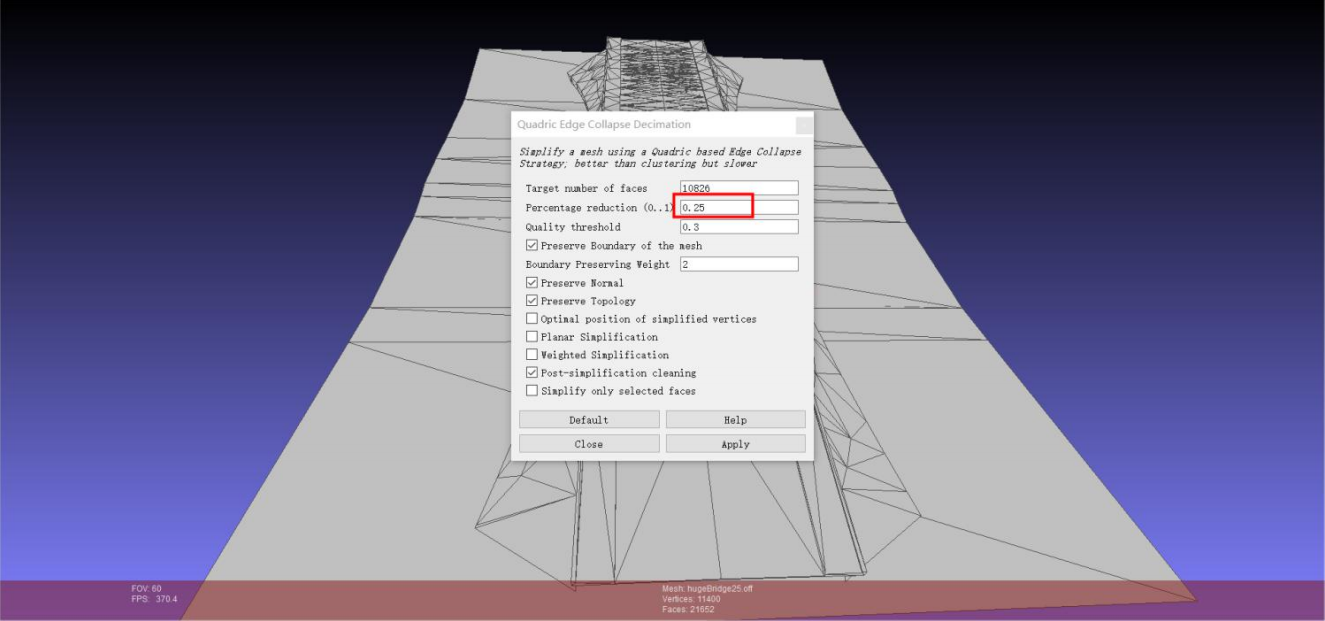
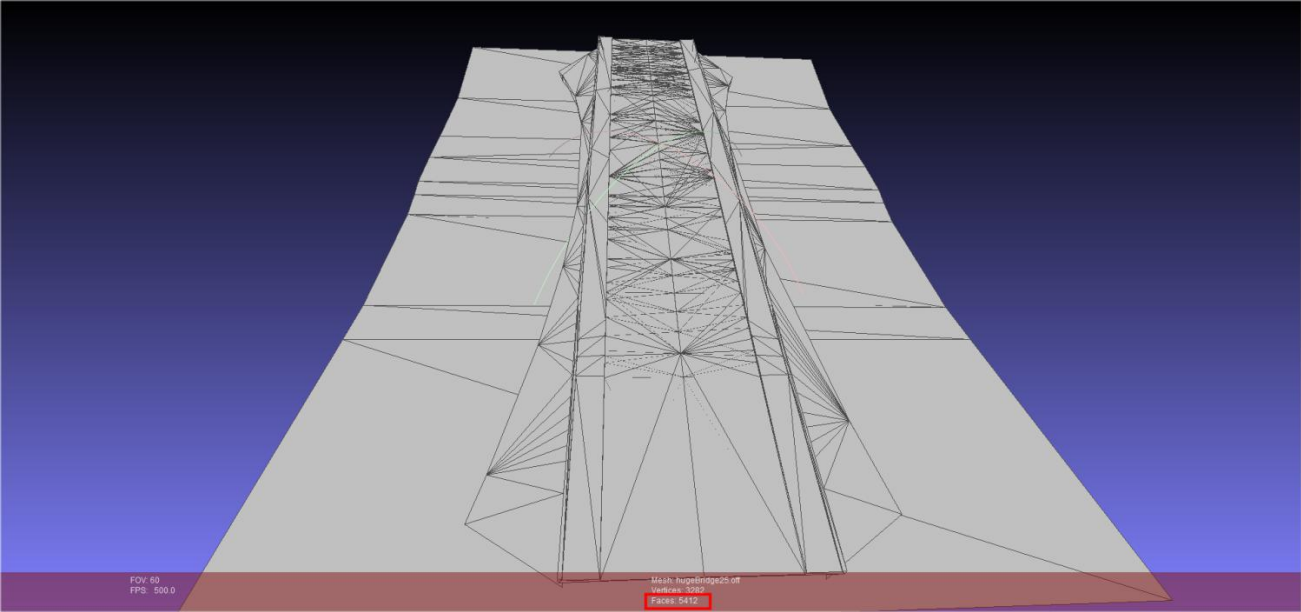
利用該算法將原有34萬+面的三維模型分別簡化為16萬、8萬、4萬、2萬、1萬個面,從圖像上的直觀上看幾乎沒有區別。技術團隊也針對簡化後的模型計算了投影面積,並測量了計算時間,總結如下表:
頂點數量 面數量 面積/平方毫米 計算時長/秒
原始數據 173926 346459 5340510605 158 已驗證
1/2簡化 80630 159992 5340510605 119 已驗證
1/4簡化 40584 80000 5340510605 64 已驗證
1/8簡化 20518 39999 5340510604 24 已驗證
1/16簡化 10391 20000 5340510885 10 已驗證
1/32簡化 5289 9999 5340510877 4 已驗證
從結果中可以看出,即使簡化為1萬個面,計算出來的面積與原始數據的偏差只有200平方毫米。
2.2.3初步結論
①針對該問題,通過採用比較成熟的開源計算方案,計算效率可以得到大幅度提高,從16分鐘縮短到3分鐘之內。
②網格簡化算法能進一步加速計算,最快4s可以得到結果,誤差微乎其微。
三、接口設計思路
希望以新接口替代超圖的GeoModel3D.convertToRegion(),所以設計入參:GeoModel3D,return:GeoRegion
實現路徑:GeoModel3D-->骨架(頂點串及序列)-->meshlab 接口接受的數
據結構(off)-->簡化網格-->節點降維-->重合處三角合併-->轉換GeoJSON -->GeoRegion
三、代碼實現
3.1 獲取三維模型構件點集
獲取超圖 Model 對象的頂點集合與序列並輸出 off 格式文件的方法參考以下代碼:
/**
* 將 Model 對象轉換為 off 格式並在指定位置輸出
*
* @param model Model 對象
* @param originalOffPath off 輸出路徑
*/
private void outputOffFile(Model model, String originalOffPath) {
List<Double> verticesList = new ArrayList<>();
List<Integer> vertexIndexesList = new ArrayList<>();
//獲取 GeoModel3D 頂點點串與序列
for (int index = 0; index < model.getSkeletonCount(-1); index++) {
SkeletonID id = new SkeletonID(-1, index);
Skeleton skeleton = model.getSkeleton(id);
double[] vertices = skeleton.getVertices();
List<Double> tempVerticeList = Doubles.asList(vertices);
verticesList.addAll(tempVerticeList);
int[] vertexIndexes = skeleton.getVertexIndexes();
List<Integer> tempIndexlist = Ints.asList(vertexIndexes);
vertexIndexesList.addAll(tempIndexlist);
}
//輸出 originalOff.off
writeOff(verticesList, vertexIndexesList, originalOffPath);
}
注意:此處的代碼 getSkeletonCount()和 SkeletonId()方法中的 LOD 層級取值-1 代表當前 LOD 層級,此種取值是約定俗成的。
3.2 Windows環境調用meshlabserver方法
我們應用meshlab的Quadric Edge Collapse Decimation方法對模型骨架轉化得到的off文件進行模型簡化。為將這部分工作做代碼實現,我們通過Meshlab的.mlx腳本,保存對原數據的操作,然後通過調用meshlabserver進行批量處理。
3.2.1 meshlab方法參數研究
在 做 三 維 模 型 簡 化 時 , 主 要 使 用MeshLab的Quadric Edge Collapse Decimation方法,其參數較多,經過試驗,建議以下參數配比:
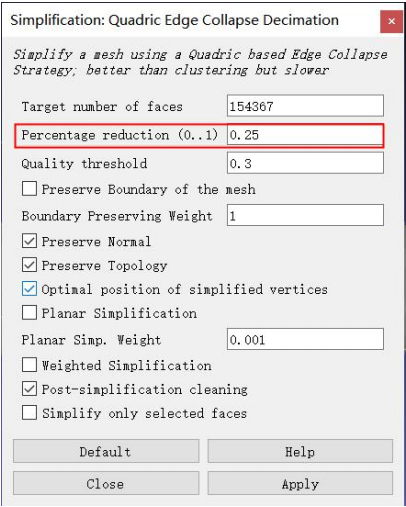
其中,需要注意的參數有以下幾個:
①Target number of faces:目標面數。簡化目標面的數量,該參數決定了簡化的程度,軟件中針對特定模型進行手動操作尚可,代碼實現需要頻繁改變腳本參數,不適用。
②Percentage reduction (0..1):簡化百分比。默認為0,當設置不為0時,簡化面數是以該參數為主,替代Target Number of Faces,如此可以跳過動態編輯mlx腳本,減少運行時間。且根據經驗,最好設置為0.5的整數次冪。
③Preserve Topology:保留拓撲關係。因為模型可能存在複雜的拓撲關係,簡化後的模型進行投影后,希望保留其應有的島洞關係,因此此處勾選。
其餘參數,默認值即可。
 -->
-->
3.2.2 meshlabserver命令行執行
如圖為meshlabserver在Windows上的cmd調用實現:
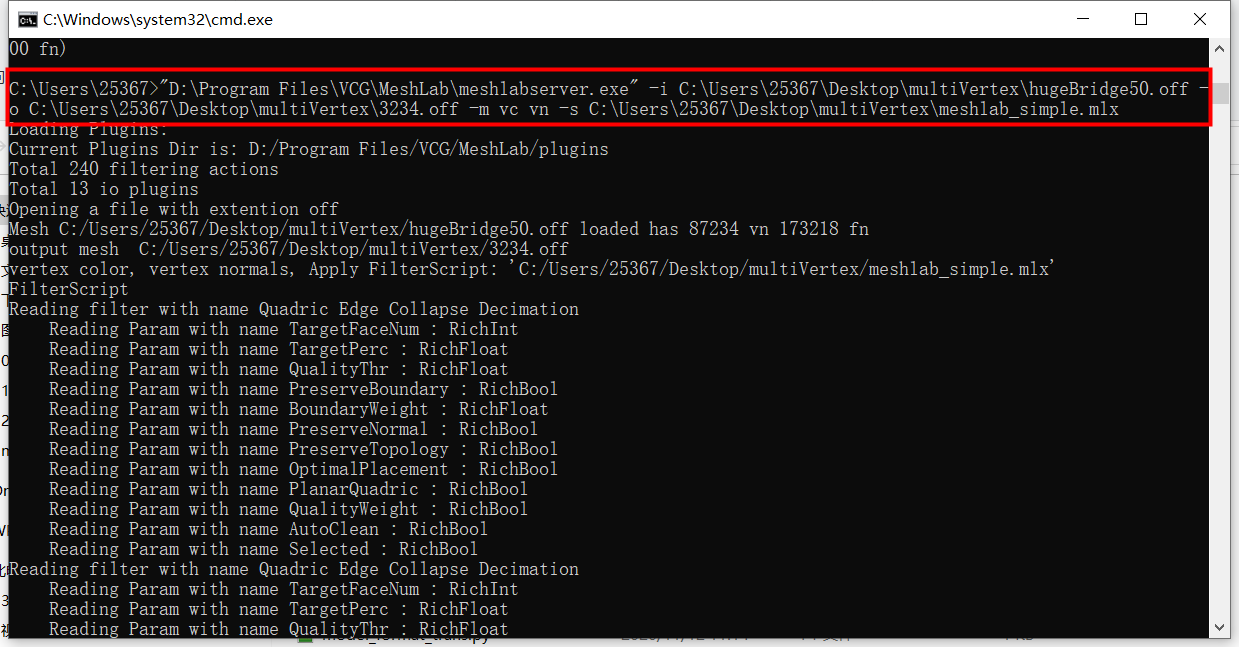
cmd 語法為:
"meshlabserver 路徑" -i 原始 off 路徑 -o 簡化輸出 off 路徑 -m vc vn -s mlx
腳本路徑
如此得到簡化off後,python讀取其中的頂點位置與序列信息,進行降維與投影合併。
3.3 python庫導入
為實現三維骨架點串的節點降維、重合處三角合併、聚合後二維圖形面積獲取等階段性目標,需要導入若干python庫,首先安裝python,3.8版本即可。
導入shapely庫,使用unary_union()做投影面合併;導入geojson庫,實現
shapely.Polygon轉化為GeoJSON文件。使用pip install命令安裝以上庫即可。
① shapely
② geojson

3.4 off的降維合併與輸出
簡化後的off,python讀取其點串信息,降維構件二維面,並調用shapely
庫的unary_union()方法實現面的合併,代碼如下:
def get_projection_area(vertices, triangles):
polygons = []
for i1, i2, i3 in triangles:
p1 = vertices[i1]
p2 = vertices[i2]
p3 = vertices[i3]
poly = Polygon(((p1[0], p1[1]), (p2[0], p2[1]), (p3[0], p3[1])))
if not poly.is_valid:
continue
polygons.append(poly)
print("polygon contructed")
unioned = unary_union(polygons)
print("unioned")
print("Area: %f" % unioned.area)
return unioned
求得合併投影面後,轉換為GeoJSON格式,以供構建超圖GeoRegion使用。
代碼如下:
def write_geojson(polygon, output_path):
#p = wkt.loads((str)(polygon))
# using geojson module to convert from WKT back into GeoJSON format
geojson_out = geojson.Feature(geometry=polygon, properties={})
with open(output_path, 'w') as outfile:
json.dump(geojson_out, outfile, indent=3)
outfile.close()
3.5 超圖GeoRegion構建與座標轉換
由於3.1中得到Model及骨架中的點集不含座標系信息,所以在此基礎上進行一系列計算得到的結果GeoRegion也是原點在o處的模型的投影面。因此合併投影面GeoJSON在轉換回超圖的GeoRegion對象後,需要根據其原始的空間矩陣做矩陣轉換,恢復位置、比例、姿態,賦予空間信息。矩陣轉換代碼如下:
/**
* 對Model骨架點串簡化投影合併得到的GeoRegion進行轉化,使其恢復位置、比例、姿態
*
* @param geoRegion 網格簡化與unary_union()後獲得的結果GeoRegion對象
* @param transformParams 矩陣轉換所需的參數
* @return 轉換後的GeoRegion
*/
private GeoRegion transformGeoRegion(GeoRegion geoRegion, TransformParams transformParams) {
GeoRegion resGeoRegion = new GeoRegion();
if (null == geoRegion || geoRegion.isEmpty()) {
return resGeoRegion;
}
try {
for (int i = 0; i < geoRegion.getPartCount(); i++) {
Point2Ds point2Ds = geoRegion.getPart(i);
Point2Ds point2DsNew = new Point2Ds();
for (int j = 0; j < point2Ds.getCount(); j++) {
Point2D point2D = point2Ds.getItem(j);
Double x = point2D.getX();
Double y = point2D.getY();
//<1>縮放
Double xRes1 = x * transformParams.getScaleX();
Double yRes1 = y * transformParams.getScaleY();
//<2>旋轉
//繞x軸
Double yRes2 = yRes1 * Math.cos(transformParams.getRotateX());
//繞y軸
Double xRes2 = xRes1 * Math.cos(transformParams.getRotateY());
//繞z軸
Double xRes3 = xRes2 * Math.cos(transformParams.getRotateZ()) - yRes2 * Math.sin(transformParams.getRotateZ());
Double yRes3 = yRes2 * Math.cos(transformParams.getRotateZ()) - xRes2 * Math.sin(transformParams.getRotateZ());
//<3>平移
Double xRes4 = xRes3 + transformParams.getOffsetX();
Double yRes4 = yRes3 + transformParams.getOffsetY();
Point2D point2dNew = new Point2D(xRes4, yRes4);
point2DsNew.add(point2dNew);
}
resGeoRegion.insertPart(i, point2DsNew);
}
} catch (Exception e) {
e.getMessage();
}
return resGeoRegion;
}
四、測試
將目前的方法與超圖convertToRegion()方法計算結果對比(在表中取形狀複雜的構件進行測試),分別比較各自投影面的面積相似度與空間覆蓋率,結果較為理想。
測試結果:
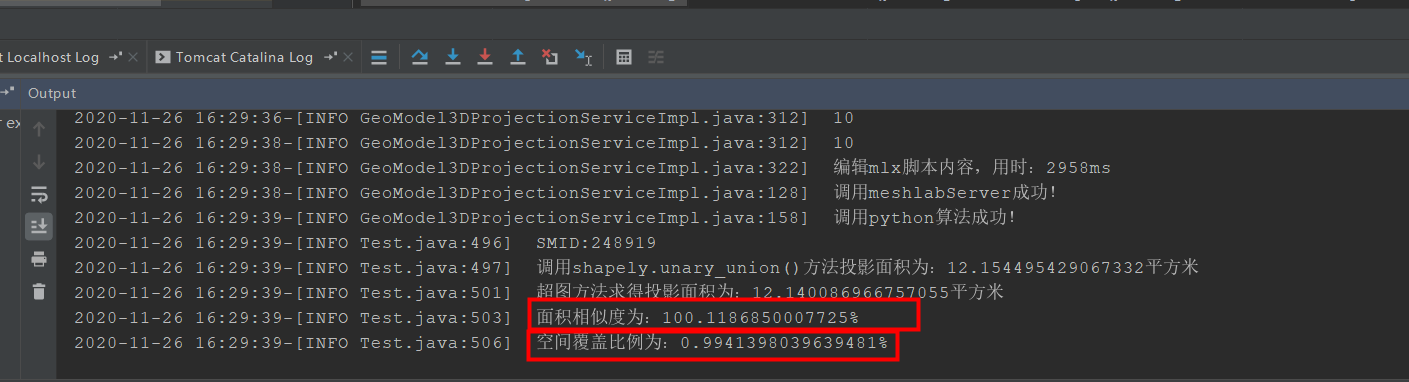
最終結果與超圖convertToRegion()方法獲取的GeoRegion比對不僅面積值
相差小,且基本重合,可知思路正確。但可供測試的超大頂點模型構件數量有限,
且測試構件複雜度不足,仍需獲取更多複雜構件進行進一步測試並優化方案。