開發與維運

圖解 赫夫曼編碼?(赫夫曼大叔開講啦！！！） | 算法必看系列二十六

2020-04-28

原文鏈接

小禹禹，你知道赫夫曼樹嗎？不知道哎！

那景禹今天就給你細細道來，在介紹赫夫曼樹之前，我們一起先來弄清楚和樹有關的四個概念。

概念一：什麼結點的路徑長度？
從根結點到該結點的路徑上的連接數。

小禹禹：還是不知道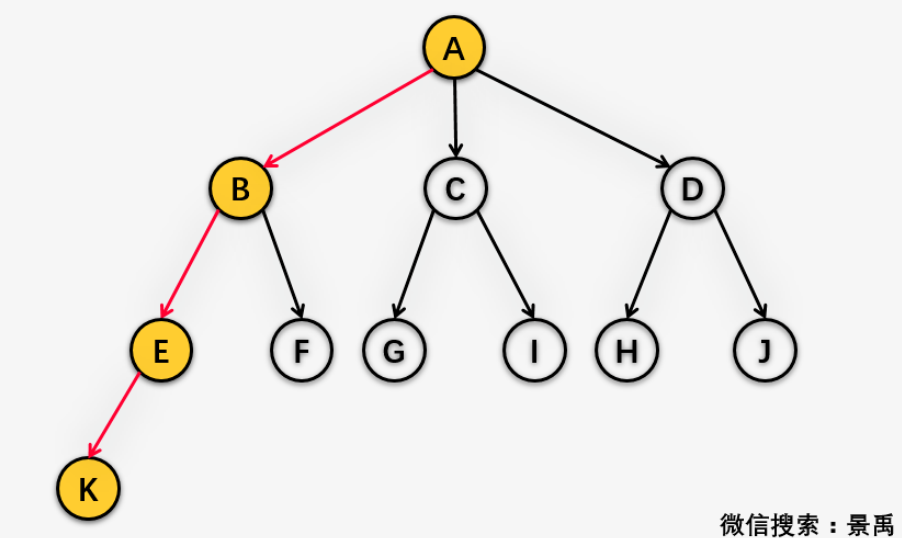
image.png
結點K的路徑長度就是從根結點A到結點K的路徑上的連接數，也就是我們看到紅色連邊，當然就是3嘍！

小禹禹（原來如此）
概念二：什麼是樹的路徑長度呢？
樹中每個葉子結點的路徑長度之和！
小禹禹：這個簡單，就是葉子結點K、F、G、I、H和 J 各自的路徑長度加起來唄 ！

很聰明麼，就是3+2 * 5=13啦！結點K的路徑長度為3，其他5個結點的路徑長度都是2。

概念三：什麼是的結點帶權路徑長度？
結點的路徑長度與結點權值的乘積。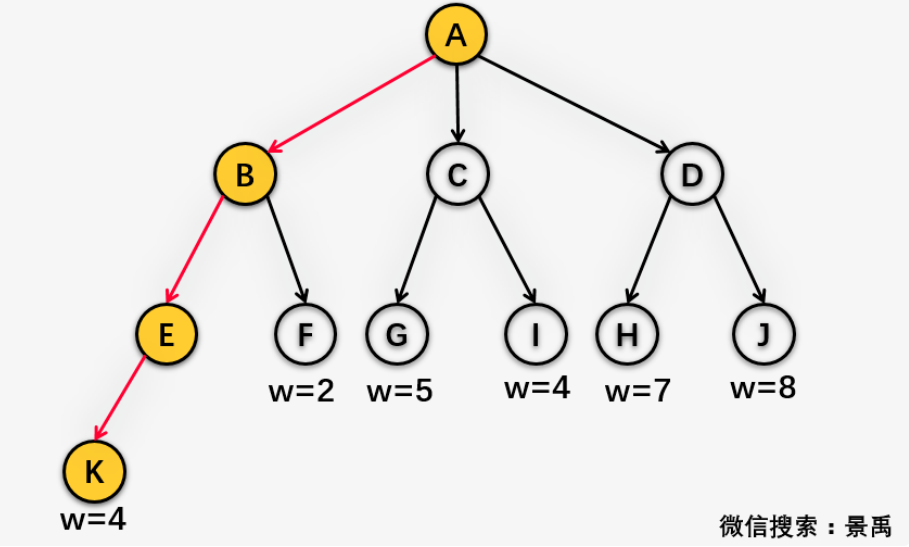
image.png
結點K的路徑長度為3，權重w=4，所以結點K的帶權路徑長度為3 * 4 = 12

概念四：什麼樹的帶權路徑長度?
WPL(Weighted Path Length)是樹中所有葉子結點的帶權路徑長度之和。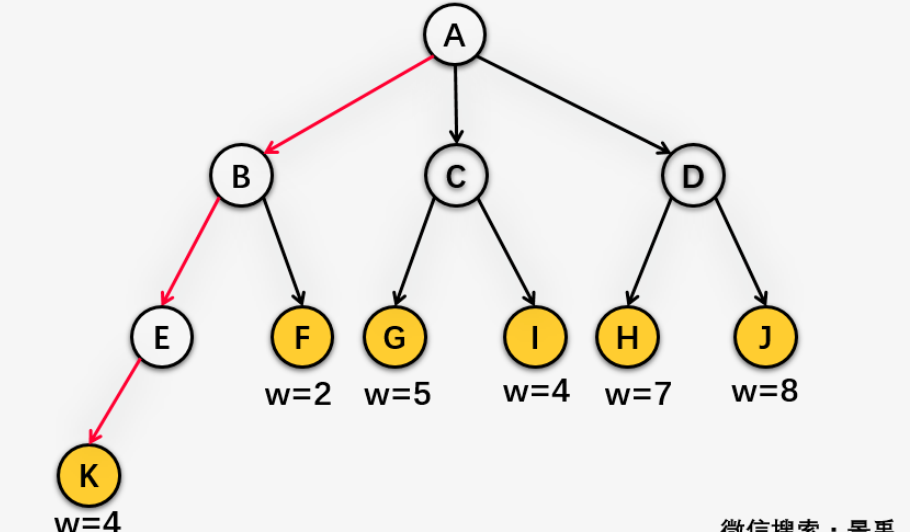
image.png
對比樹的結點路徑長度，樹的帶權路徑長度=3 4 + 2 （2+5+4+7+8）= 64 （哈哈，景禹是不是故意給我整一個這麼有意義的數字的）就是啦，準確無疑~~

小禹禹：天呢，一棵樹上還有這麼多東東！

樹：哈哈，因為我厲害呀，你們需要我，我不多給自己增加些分量怎麼行？

為了給大家講清楚赫夫曼樹，今天景禹請來了我們麻省理工學院的赫夫曼大叔，景禹先拍一拍赫夫曼大叔的馬屁。

在數據膨脹、信息爆炸的今天，數據壓縮的意義不言而喻。談到數據壓縮，就不能不提赫夫曼（Huffman）編碼，赫夫曼編碼是首個實用的壓縮編碼方案，即使在今天的許多知名壓縮算法裡，依然可以見到赫夫曼編碼的影子。

另外，在數據通信中，用二進制給每個字符進行編碼時不得不面對的一個問題是如何使電文總長最短且不產生二義性。根據字符出現頻率，利用赫夫曼編碼可以構造出一種不等長的二進制，使編碼後的電文長度最短，且保證不產生二義性。

下面有請我們的赫夫曼博士本人給你介紹一下自己的成果。

前面景禹給小禹禹介紹了WPL，我就不在此陳述了，需要指出的是：WPL的值越小，說明構造出來的二叉樹性能就越優。我當初就死命的塗塗畫畫，最終研究出了一種最優的構造方法，我也挺辛苦，就以自己名字命名為赫夫曼樹，小禹禹先來看一下赫夫曼樹的構造過程。

首先我給你們給出一個初始森林，如下圖：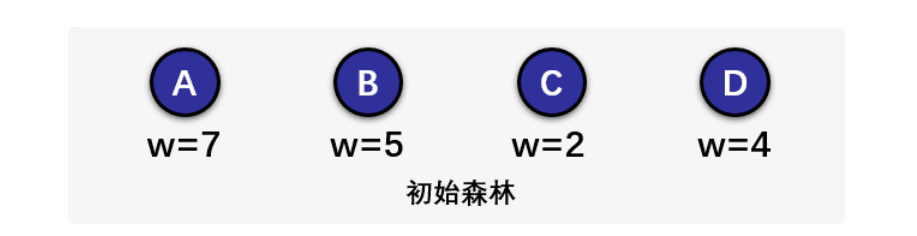
image.png
第一步：森林中選擇出兩顆結點的權值最小的二叉樹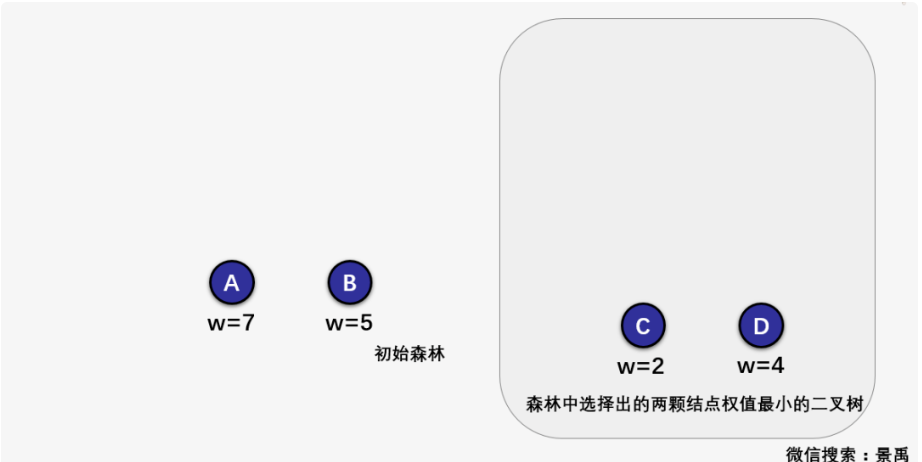
image.png
第二步：合併兩顆二叉樹，增加一個新的節點作為新的二叉樹的根，權值為左右孩子的權值之和。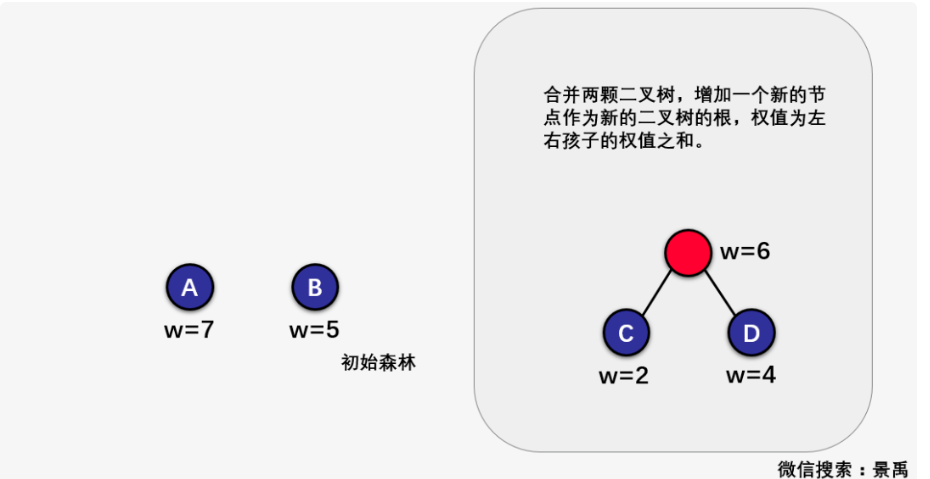
image.png
接下來就是重複以上兩步驟了，我們直接來看一下赫夫曼大叔給大家準備的動畫。

點擊查看視頻

image.png
定長編碼（fixed-length codes）：像ASCII編碼（後臺回覆：ascii 就可以獲取ASCII編碼表）、Unicode編碼。ASCII編碼每一個字符使用8個bits，能夠編碼256個字符；Unicode編碼每個字符佔16個bit，能夠編碼65536個字符，包含所有ASCII編碼的字符。

image.png
image.png
定長編碼的缺陷：

浪費空間！對於僅包含ASCII字符的純文本消息，Unicode使用的空間是ASCII的兩倍，兩種方式都會造成空間浪費；字符“ a”和“ e”的出現頻率比“ q”和“ z”的出現頻率高，但是他們都佔用了相同位數的空間。要解決定長編碼的缺陷，便有了下面的變長編碼。

變長編碼：單個編碼的長度不一致，可以根據整體出現頻率來調節，出現頻率越高，編碼長度越短。

變長編碼優於定長編碼的是，變長編碼可以將短編碼賦予平均出現頻率較高的字符，同一消息的編碼長度小於定長編碼。

image.png

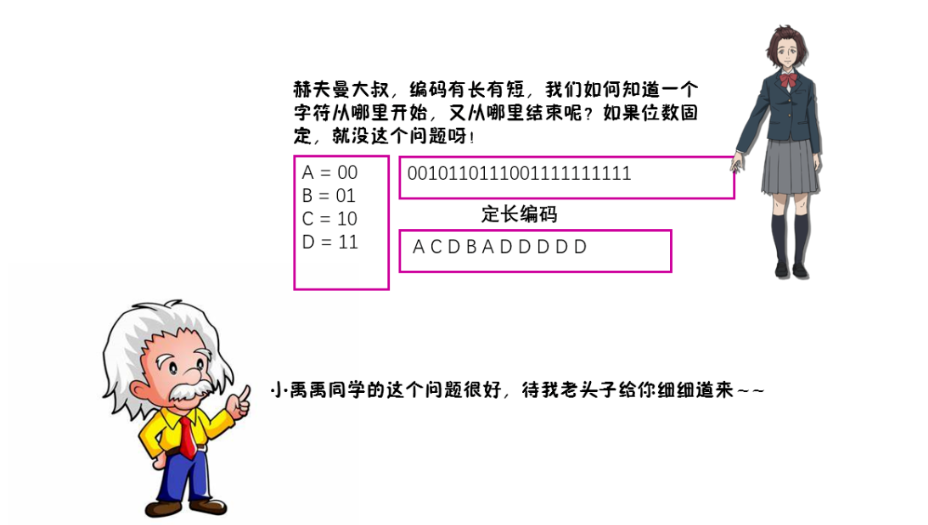
前綴屬性：

字符集當中的一個字符編碼不是其他字符編碼的前綴，則這個字符編碼具有前綴屬性。所謂前綴，一個編碼可以被解碼為多個字符，表示不唯一。比如，abcd需要編碼表示，設a=0 b=10 c=110 d=11，則表示110可以是c也可以是da。不理解沒關係，我老頭子給你準備了例子。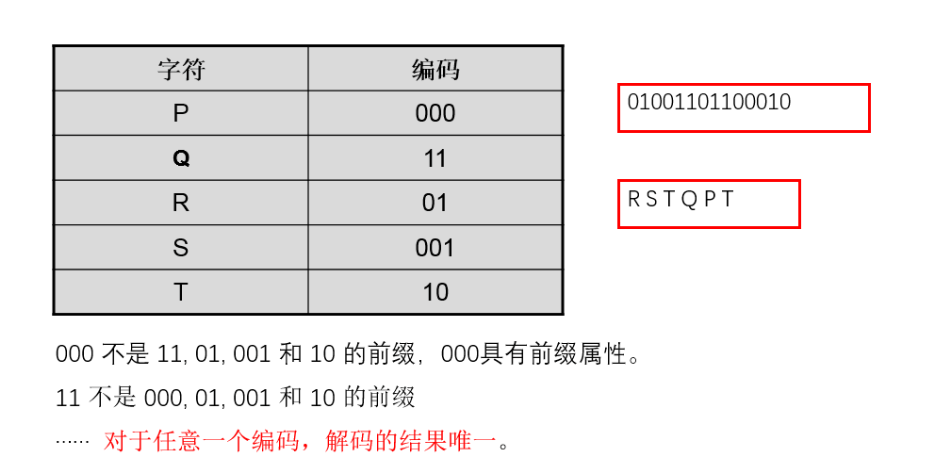
image.png
小禹禹們，還不理解，我老頭也是心累呀，那你再看下面的例子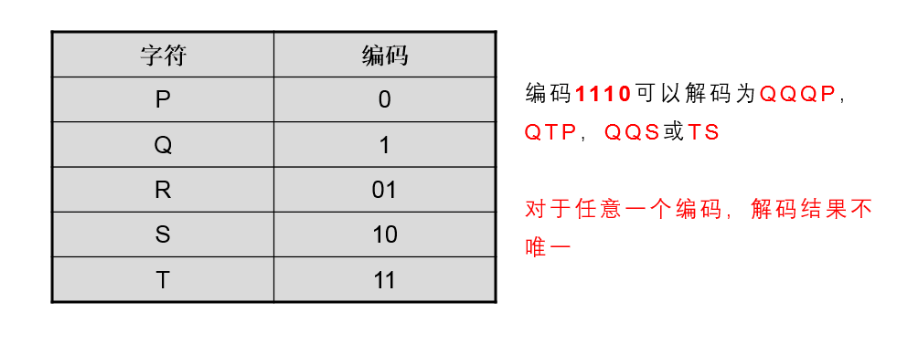
image.png
前綴碼：所謂的前綴碼，就是沒有任何碼字是其他碼字的前綴

終於解決掉了前綴屬性的問題，關於前綴碼的定義，我老頭子不給你們這些小屁孩讀了！不過得考考你們

問題：請設計變長的前綴碼，使用22位對消息DEAACAAAAABA進行編碼

赫夫曼大叔解答：使用22位對消息DEAACAAAAABA進行編碼的前綴碼編碼方案很多。消息中字符 A 出現了8次，字符 B、C、D 和 E 均只出現了1次；字符 A 用一個bit位表示，A=0，其他字符的編碼均不能以0開頭；B=10、C=110、D=1110和 E=11110；DEAACAAAAABA=1110111100011000000100，剛好22位。老頭子再給你們提供其他幾種，自己下去嘗試嘗試。

image.png
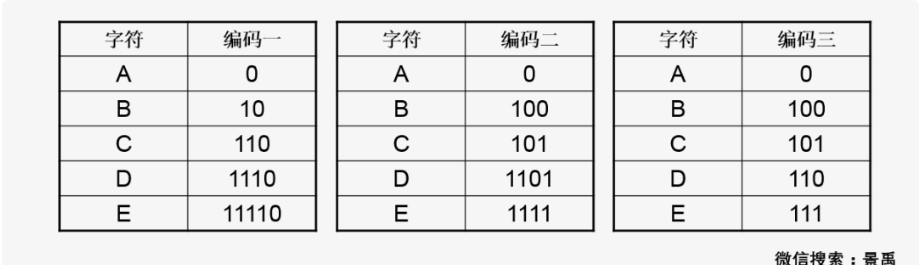
給你們鋪墊了這麼多，也該講講我老頭子自己的東西了！我所提出的赫夫曼編碼就是一種前綴碼，在進行編碼的時候，我是通過一顆赫夫曼編碼樹（Huffman coding tree）進行的，所以先來看一下我構造的這顆老頭子編碼樹的一些特性唄！

1、霍夫曼編碼樹是一顆二叉樹

  • 每片葉子結點都包含一個字符
  • 從結點到其左孩子的路徑上標記0
  • 從結點到其右孩子的路徑上標記1

2、從根結點到包含字符的葉子結點的路徑上獲得葉結點的編碼

3、編碼均具有前綴屬性

  • 每一個葉結點不能出現在到另一個葉結點的路徑上
  • 注意：定長編碼可以由完整的霍夫曼樹表示，並且顯然具有前綴屬性

有了霍夫曼編碼樹的特性，我們也知道了霍夫曼樹的構造過程，最後再給大家看一個霍夫曼編碼及霍夫曼樹構造的完整示例。

示例：建立消息 This is his message 的一顆赫夫曼編碼樹。
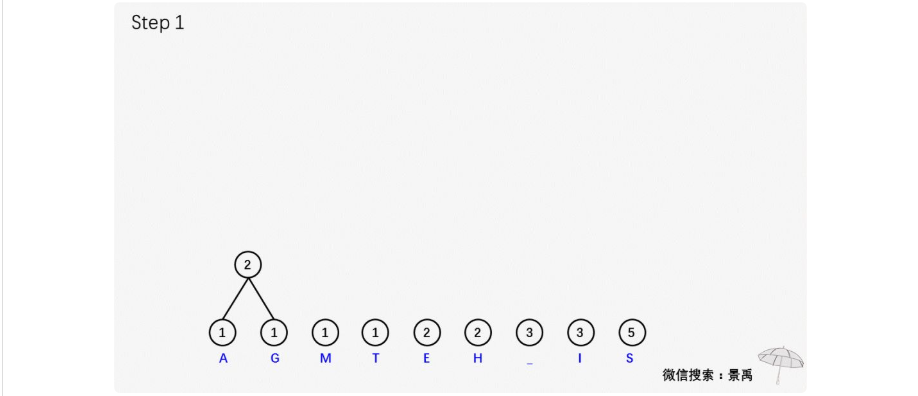
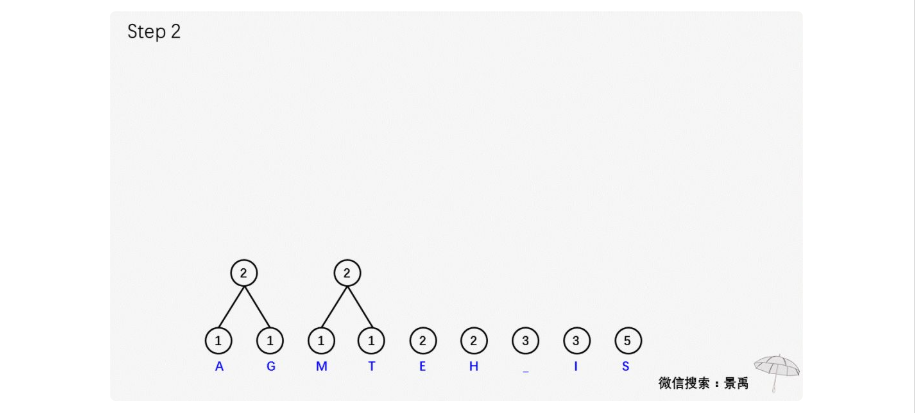
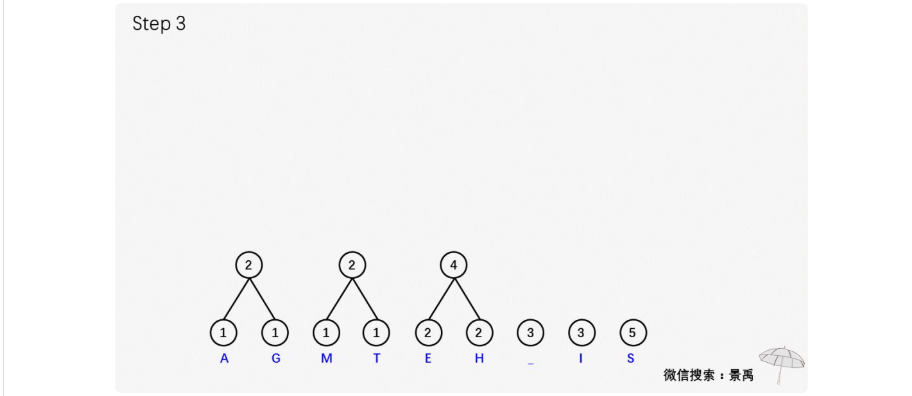
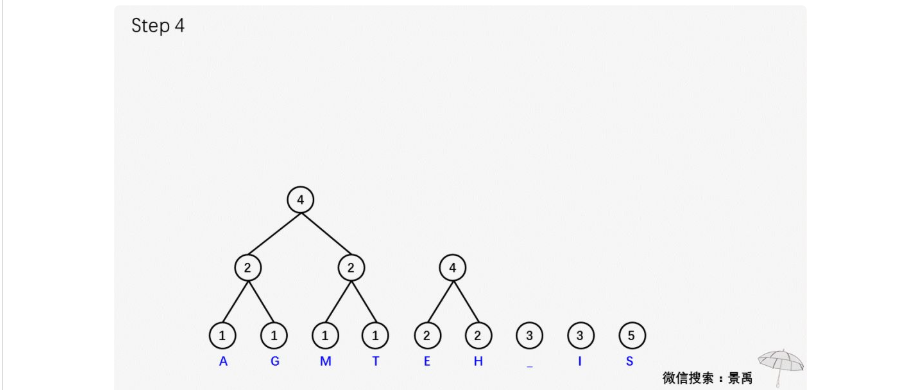
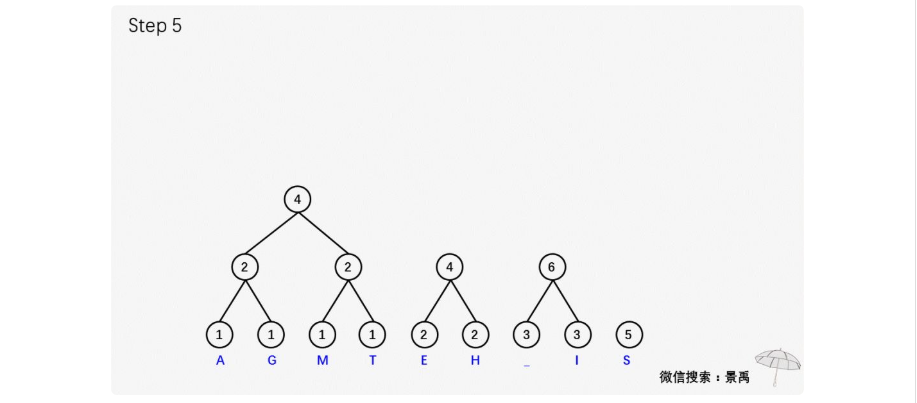
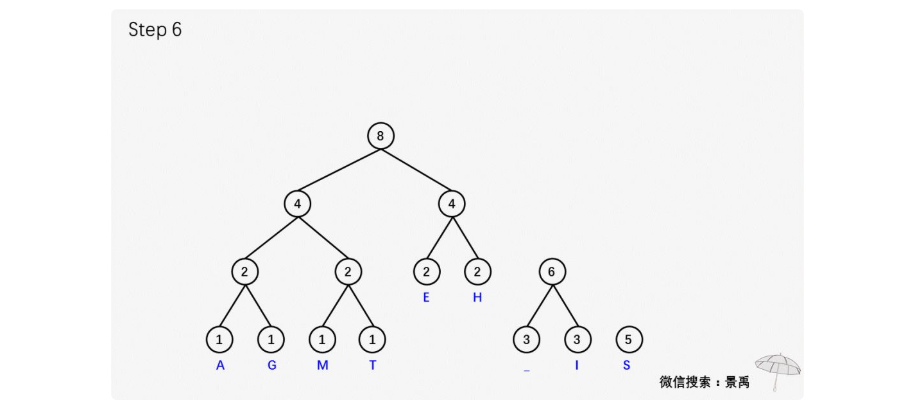
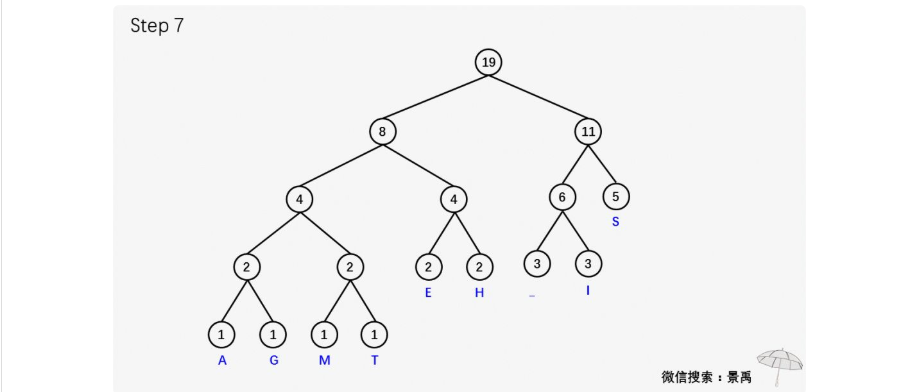
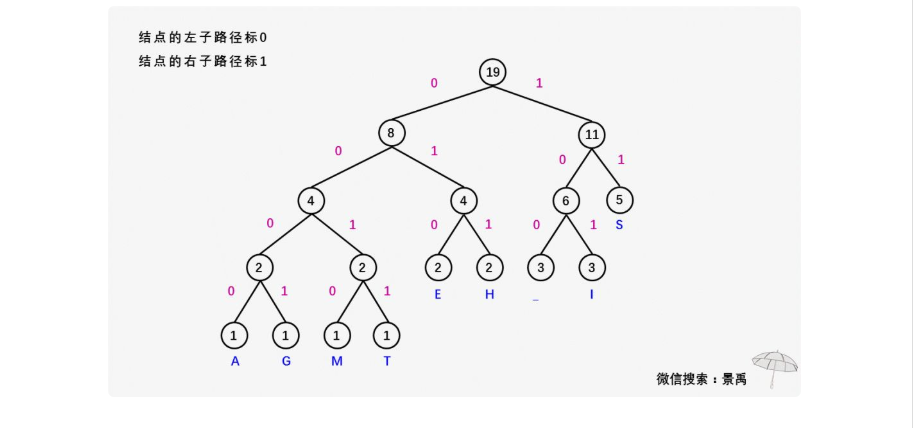
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
建立赫夫曼樹（可以對照著上面的示例看代碼）

htTree * buildTree(char *inputString)
{
  //計算字符串中每一個字符出現的次數
  //已知8個bit位可以表示256個字符
  //(256 ASCII 字符)
  int * probability = (int *)malloc(sizeof(int)*256);
  
  //初始化字符出現次數的統計數組
  for(int i=0; i<256; i++)
    probability[i]=0;

  //將每一個字符的ASCII碼值作為索引，統計字符出現次數
  for(int i=0; inputString[i]!=''; i++)
    probability[(unsigned char) inputString[i]]++;

  //使用優先隊列存儲樹中的結點
  pQueue * huffmanQueue;
  initPQueue(&huffmanQueue);

  //為字符串中的每一個字符創建一個結點，相當於初始化森林
  for(int i=0; i<256; i++)
    if(probability[i]!=0)
    {
      htNode *aux = (htNode *)malloc(sizeof(htNode));
      aux->left = NULL;
      aux->right = NULL;
      aux->symbol = (char) i;
      
      addPQueue(&huffmanQueue,aux,probability[i]);
    }

  //釋放字符出現次數的統計數組，因為優先隊列中已經存儲了，不需要了
  free(probability);

  //按照赫夫曼樹創建步驟創建赫夫曼樹
  while(huffmanQueue->size!=1)
  {
    //取出優先隊列中權值最小的兩個節點，並將它們的權值相加
    int priority = huffmanQueue->first->priority;
    priority+=huffmanQueue->first->next->priority;
    
    //優先隊列中的權值最小的兩個元素出隊並保存
    htNode *left = getPQueue(&huffmanQueue);
    htNode *right = getPQueue(&huffmanQueue);

    //創建一個新結點作為出隊的兩個節點的父親節點
    htNode *newNode = (htNode *)malloc(sizeof(htNode));
    newNode->left = left;
    newNode->right = right;
  
    //將新結點的值入隊
    addPQueue(&huffmanQueue,newNode,priority);
  }

  //創建樹根節點，並將優先隊列中最後一個值賦給根結點
  htTree *tree = (htTree *) malloc(sizeof(htTree));

  tree->root = getPQueue(&huffmanQueue);
  
  return tree;
}

得到赫夫曼樹之後，我們就可以得到字符的赫夫曼編碼了。
image.png
計算字符的赫夫曼編碼並建表：

hlTable * buildTable(htTree * huffmanTree)
{
  //初始化赫夫曼表
  hlTable *table = (hlTable *)malloc(sizeof(hlTable));
  table->first = NULL;
  table->last = NULL;
  
  //輔助變量
  char code[256];
  //k 記錄遍歷過程中的層數
  int k=0;

  //遍歷赫夫曼樹並計算字符編碼
  traverseTree(huffmanTree->root,&table,k,code);
  return table;
}

有了赫夫曼碼錶之後，就可以對輸入的字符串進行編碼和解碼了。
字符串編碼：

void encode(hlTable *table, char *stringToEncode)
{
  hlNode *traversal;
  
  printf("nEncodingnInput string : %snEncoded string : n",stringToEncode);

  //對字符串的每一個字符遍歷赫夫曼碼錶
  //當在碼錶中遇到字符，則輸出對應的字符編碼
  for(int i=0; stringToEncode[i]!=''; i++)
  {
    traversal = table->first;
    while(traversal->symbol != stringToEncode[i])
      traversal = traversal->next;
    printf("%s",traversal->code);
  }

  printf("n");
}

字符串解碼：

void decode(htTree *tree, char *stringToDecode)
{
  htNode *traversal = tree->root;

  printf("nDecodingnInput string : %snDecoded string : n",stringToDecode);

  //對於消息編碼的每一個bit位，遍歷赫夫曼樹並進行解碼操作
  //從赫夫曼的根結點開始，遇到0則走左子樹
  //遇到1則走右子樹
  for(int i=0; stringToDecode[i]!=''; i++)
  {
    if(traversal->left == NULL && traversal->right == NULL)
    {
      printf("%c",traversal->symbol);
      traversal = tree->root;
    }
    
    if(stringToDecode[i] == '0')
      traversal = traversal->left;

    if(stringToDecode[i] == '1')
      traversal = traversal->right;

    if(stringToDecode[i]!='0'&&stringToDecode[i]!='1')
    {
      printf("The input string is not coded correctly!n");
      return;
    }
  }

  if(traversal->left == NULL && traversal->right == NULL)
  {
    printf("%c",traversal->symbol);
    traversal = tree->root;
  }

  printf("n");
}

主要代碼就是四個關鍵的函數，需要注意的是，為了保證權值始終按照降序排列，我們使用了優先隊列進行存儲權值，一般也可以理解為一個小頂堆。
image.png
image.png

來源 | 五分鐘學算法
作者 | 程序員小吳

Leave a Reply

Your email address will not be published. Required fields are marked *